Harmonic Path Planning using Quarter-Sweep Boosted TOR Iterative Method

Abstract

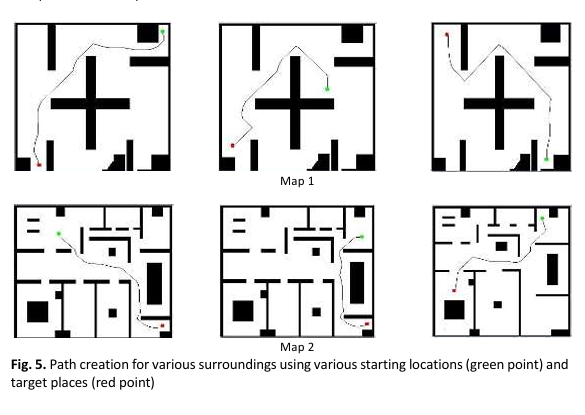
This paper presents the study to examine the effectiveness of the application of Quarter Sweep Boosted TOR with the 9-Point Laplacian operator using the families of relaxation methods in the computation of Laplace equation solutions to obtain the harmonic potentials. This work is a continuation from the past study that applied the standard application 5-Point Laplacian to solve path planning issue which a mobile robot faces because of working in indoor environment. The robot can navigate from a given initial position to a goal position by following the safest path, ensuring it avoids any obstacles and minimizes the risk of collisions. By utilizing the equation of Laplace and computing the potential values’ distribution in the environments which have been simulated, the robot can determine the safest path that avoids obstacles which exists in the environment. This method ensures that the robot moves along a path where the potential for collisions is minimized. The findings confirm that QSBTOR outperforms Half Sweep Boosted TOR (HSBTOR) and Full Sweep Boosted TOR (FSBTOR). QSBTOR and HSBTOR show 73% and 50% reduction respectively, compared to FSBTOR in terms of computational complexity.