Efficient Application of Modified TOR Iterative Method with GPU Acceleration in Robotics and Image Processing

Abstract

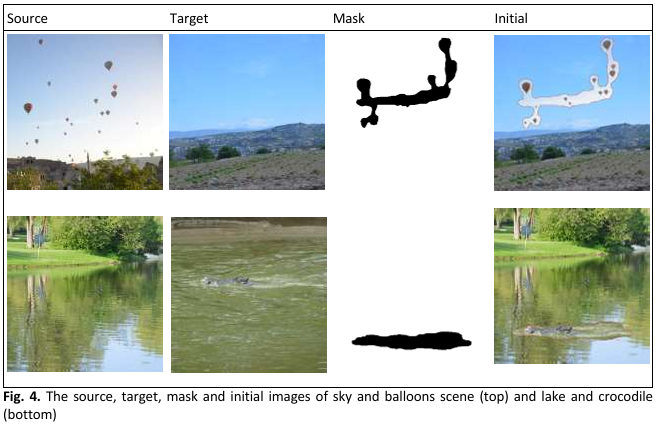
This paper presents the application of the Modified TOR (MTOR) method, implemented using CUDA, for solving Poisson's equation through the iterative Finite Difference (FD) method. The study aims to provide a detailed description of the MTOR method for solving Partial Differential Equations (PDEs) on both standard and rotated meshes, employing CUDA for parallel processing. The MTOR method uses a red-black ordering strategy during iteration; consequently, the calculation of red cells utilizes the updated values of their four neighbouring black cells, and vice versa. To evaluate the performance of these iterative methods, robot path planning and image blending problems were tested. Our results highlight the advantages of employing parallel methods on Graphics Processing Units (GPUs) in terms of iterations and computational time, compared to their sequential counterparts. In the path planning simulation, the parallel implementations exhibited over 20 times faster execution compared to their corresponding sequential versions. Similarly, in the image blending problem, the parallel implementations achieved more than a 6-fold improvement in speed compared to the sequential methods.