Performance Analysis of Log-Space Harmonic Potentials for Path Planning in Indoor Environment

Abstract

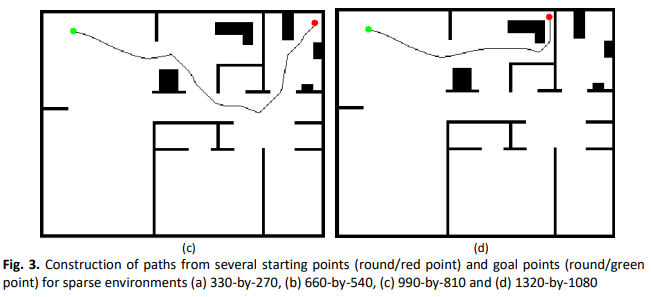
In recent years, there has been an increasing interest in the study of path planning algorithms for autonomous robot systems. The current study aims to examine the simulation performance of path planning using the Successive Overrelaxation (SOR) method and the log-space Gauss-Seidel (LGS) method. The simulation addresses the numerical solution of a boundary value problem for Laplace's equation, utilising Log-space mapping and adhering to Dirichlet boundary conditions within a closed region. The experiment done in both sparse and dense environments shows the benefits of the iterative methods. The paths generated by the SOR and LGS approach are compared using specific numerical examples in smooth trajectory planning. The comparative analysis suggests that the LGS iterative method effectively addresses the issue of achieving high precision in the numerical computation of the gradient of harmonic potentials for generating safe paths in dense environments with narrow corridors and difficult regions. The simulation results also indicate that the LGS employed in this study exhibits faster convergence. Although it has a slower execution time, it is successful in dense environments compared to the SOR method.