Minimization of DNA String using Shortest Path Problem

Abstract

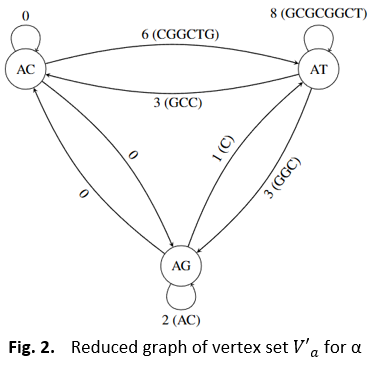
The structure of deoxyribonucleic acid (DNA) consists of two nucleotides chained together where nucleotides are long strands of DNA bases, namely Adenine (A), Cytosine (C), Guanine (G) and Thymine (T), linked together by sugar and phosphates molecules. DNA molecule can be represented by a graph as a mathematical model. In graph theory, finding the shortest path between two vertices in a graph is called the shortest path problem. In this research, a DNA string is represented in graphical form so that the shortest path problem can be applied to minimize the DNA string. The vertex of the graphical form of a DNA string is formed by base pairs of length two, while the shortest length of bases between the vertices acts as the edges of the graph. In this process, four graphs are formed, classified by four initial bases used for the vertices. From the graphs generated, the shortest path for all vertices is calculated where any untraversed path is removed from each of the graphs, forming a simplified graph for each case. Next, by finding the Euler path for the simplified graph and converting the path taken back into a DNA string, a minimized DNA string is formed. From the results, it is shown that, the graph with initial base of T produces the shortest minimized DNA string while the graph with initial base of C produces the longest minimized DNA string.