Solute Dispersion in Casson Blood Flow through a Stenosed Artery with the Effect of Temperature and Electric Field
DOI:
https://doi.org/10.37934/arefmht.17.1.1434Keywords:
Blood flow, Casson fluid, electric field, Generalized Dispersion Model, solute dispersion, temperatureAbstract
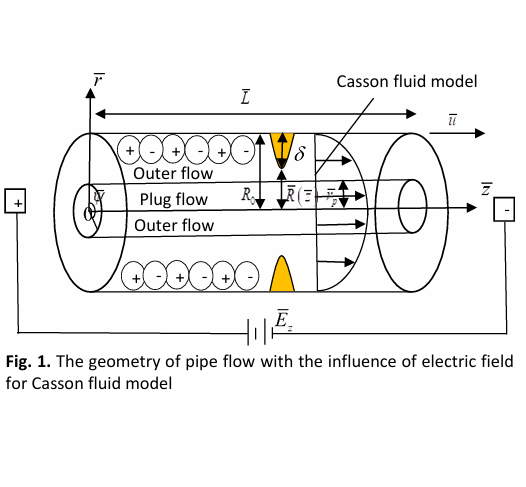
This study develops a mathematical model to address solute dispersion in arterial blood flow, particularly considering the effects of temperature and electric fields using the Casson fluid model. Given the physiological importance of drug delivery within the human vascular system, understanding these dynamics is crucial, especially in the presence of cardiovascular diseases (CVD). The Generalized Dispersion Model (GDM) is employed to simulate the dispersion function. Results demonstrate that elevated temperatures and electric fields enhance drug uptake and distribution by increasing blood flow. The model accurately predicts drug behavior in narrowed arteries, optimizing dosage regimens and improving therapeutic outcomes. Visual representations and detailed discussions of these findings are presented in the subsequent sections. The results are validated against a previous study that did not consider the effects of stenosis height, temperature and electric field. The findings suggest a strong agreement between the two studies. Additionally, an increase in mean absorption leads to an increase in velocity. When mean absorption increases, the functions of steady dispersion and overall dispersion decrease, while the function of unsteady dispersion increases. The reverse behavior is observed for the electric field. The study concludes that integrating temperature and electric field effects into drug delivery systems can significantly enhance treatment efficacy and reduce side effects, providing a valuable tool for advanced targeted therapies in CVD and cancer management.
Downloads