Advection-Diffusion Equation with Spatially Dependent Coefficients for Instantaneous Pollutant Injection in a River

Abstract

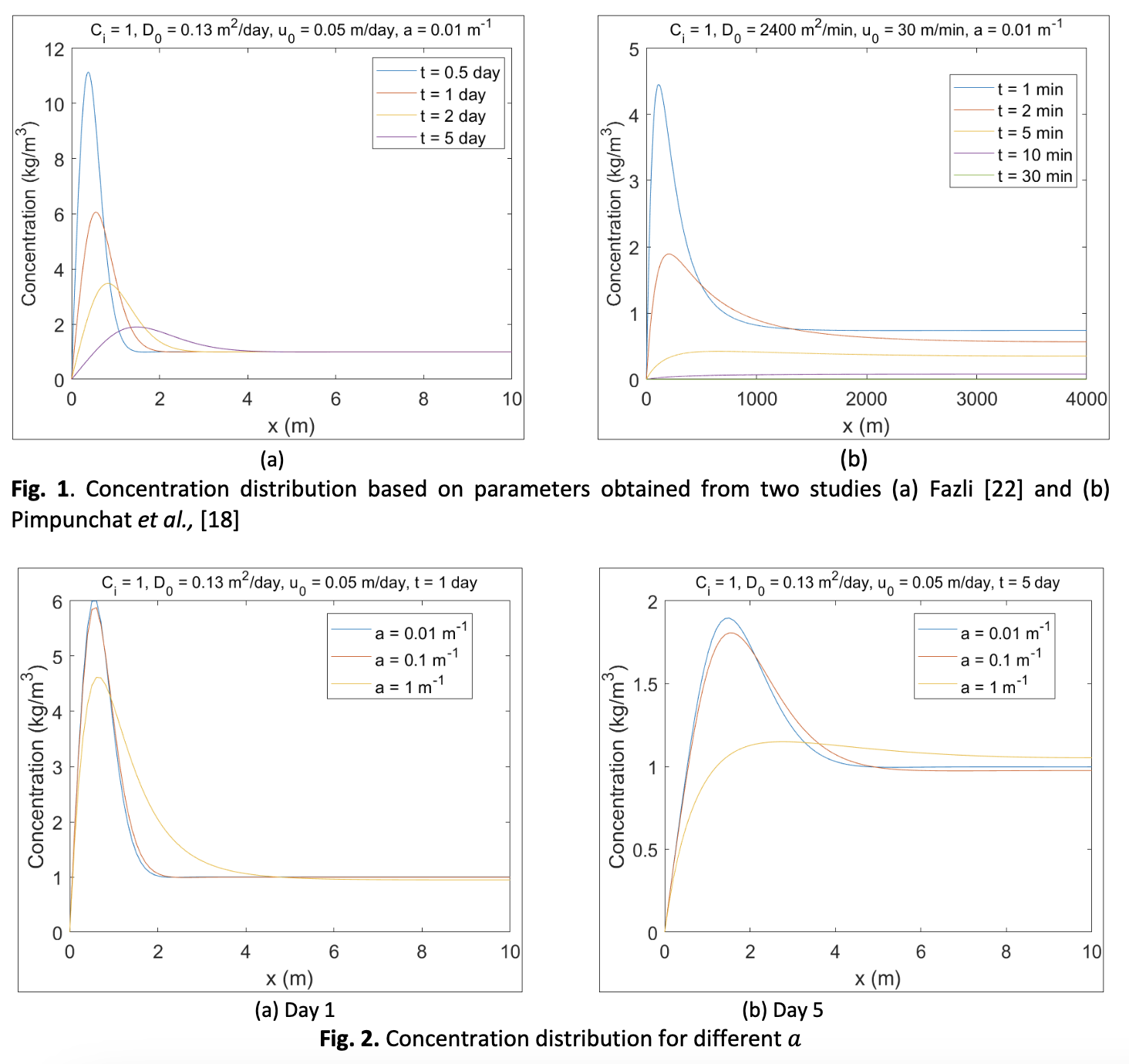
River pollution is a major environmental concern globally, affecting ecosystems and water quality. Numerous strategies have been implemented to monitor and mitigate pollution, including mathematical modeling techniques. Among these, the advection-diffusion equation (ADE) has been widely applied to model the transport and dispersion of pollutants in rivers. Previous studies on the ADE have primarily examined pollutant concentration in rivers under scenarios where pollution enters the river continuously from the boundary or, if not continuous, is modelled with exponential decay in concentration. However, pollution in real situations can often be introduced to the river instantaneously. Furthermore, it has been demonstrated that the dispersion of the pollutant and the river velocity are not constant but varies with position (space). This research focuses on finding the analytical solution to the one-dimensional ADE with spatially dependent diffusion and velocity for the case where the pollutant is instantaneously introduced to the river. New space variables are introduced in the solution procedures to reduce the ADE to a simpler form with a single coefficient which is then solved using Laplace transform method. The findings demonstrate that velocity, diffusion coefficient, and medium inhomogeneity significantly influenced the pollutant concentration distribution in rivers. Since the pollutant is instantaneously injected, the peak concentration occurs not at the source of injection but at nearby location. While the spatially dependent effect with larger inhomogeneity demonstrates a much faster and broader pollutant distribution.