A Scheme Associated with Newton-Cotes of Order One for Solving the Linear Goursat Problem Involving Derivative Term

Abstract

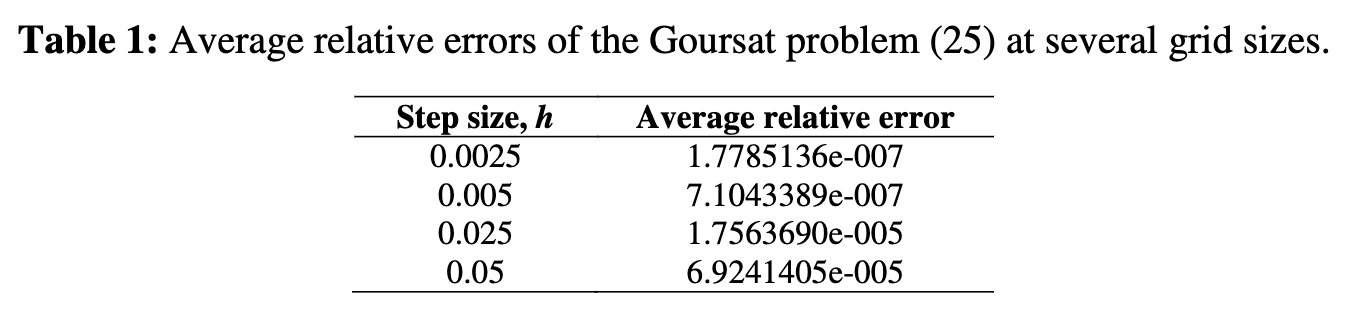
The Goursat partial differential equation is a second order hyperbolic equation that arises in several fields of study. Various numerical methods have been investigated by researchers for solving the Goursat problem such as Adomian Decomposition method, Sumudu Decomposition method, Arithmetic Mean scheme, Centroidal Mean Averaging scheme and Heronian Mean scheme. The purpose of this paper is to develop a new scheme associated with Newton-Cotes of order one for solving the derivative linear Goursat problem. The linear operators and Newton-Cotes of order one are utilized in developing the scheme. The approximation of the derivative term in the functional value plays a big role in providing a good numerical solution for the problem. The high level of accuracy obtained from the numerical experiments validates that the scheme is fit in solving the linear Goursat problem involving derivative term. The comparative study also proved that the scheme has provided a good approximate solution by presenting a better result compared to the results from previous studies. Hence, the accuracy level obtained from the numerical experiments validates the efficiency and reliability of the proposed scheme towards the Goursat problem involving derivative term.