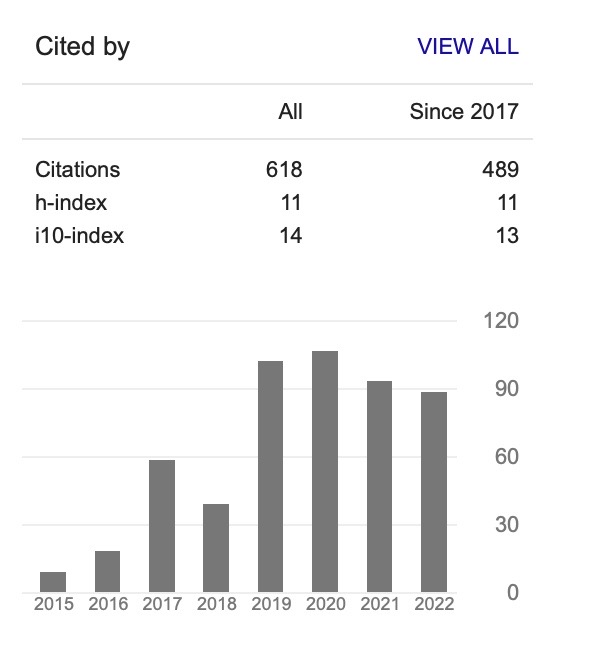
A Bounded Lorentzian Estimation for an Iterative Tomographic Imaging Reconstruction Supported with Lorentzian Regularization

Abstract

Considerable contributions are recently focused on computed tomography (CT) reconstruction methods. Since traditional algorithms based on L2 norm are commonly used, they may degrade the resulting image instead of improving it. In this paper, a bounded-influence M-estimator algorithm based on lorentzian norm has been proposed. Using lorentzian norm for tomographic imaging reconstruction suppresses the outliers due to violations of the observation model while preserving the crispness details. Furthermore, the proposed calculation not only enhances the recreated picture but also upgrades the smoothness constraint where the regularization step is connected with a specific end goal to expel the artifacts from the picture occurring because of associated noise. Experimental results demonstrate that the suggested tomographic imaging calculation has superior robust performance comparing to L2 estimation with L2 regularization model.